Why gyros loose some of their weight ? How to make real flying saucer ? And nature of gravity !

English

На тази, и на следващата страница ще се опитам да ви изложа възгледите си относно упоменатите вече тези

 с възможно най-минималния и достъпен математически апарат.

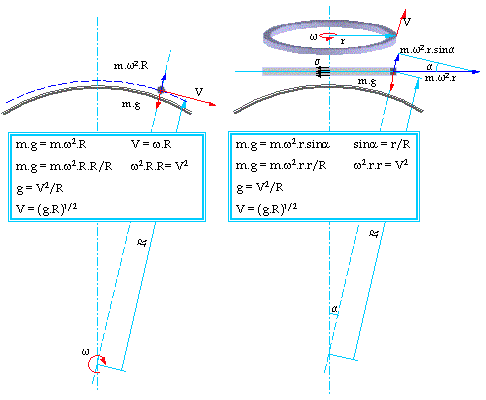
   Но първо, за да сме наясно с най-общия принцип на орбитално движение нека започнем с разглеждане на класическия случай на тяло движещо се на орбита около земята и силите които му въздействат (рис.1 ляво).

   Това са силите на тежестта m.g и центробежната сила m.V2/R. Необходимото условие за да се движи тялото на зададената орбита е двете сили да са в равновесие. След кратки преобразования (рис.1 ляво) се вижда, че за да се изпълни условието е единствено необходимо тялото да се движи със скорост V=(g.R)1/2 (нека я наречем орбитална), без значение от масата си.

   Нека сега да разгледаме силите които въздействат на тяло с форма пръстен с радиус r и маса  m който се върти с периферна скорост V=w.r. Тъй като земята е с форма на сфера нашият пръстен е в същото време и основа на конус  и всяка частица от него е на разсточние R от върха му (центъра на земята), и на всяка действа силата на тежеста m.g и центробежната сила m.w2.r.  Kакто се вижда от (рис.1 дясно) тя има проекция m.w2.r.sina насочена в посока противоположна на силата на тежестта.

   И от тук започва наистина интересната част. Нека видим какво е необходимо тези две сили да са в равновесие? След кратки преобразования (рис.1 дясно), отново получаваме че единствено необходимото условие е периферната скорост на нашия пръстен да бъде V=(g.R)1/2. Резултат който ни е познат и получихме и по-рано при класическото орбитално движение.

   Масата няма значение, а също така и размера на пръстена, просто при достигане на същата периферна скорост нашият пръстен би трябвало да започне да левитира!

pic.1

   Дотук всичко изглежда нормално и вече можем да кажем че, имаме движител за нашия леателен апарат.

   По-долу ще разгледаме и някой от възможните начини за създаването му, и възможните препятсвия по пътя на неговата практическа реализация.
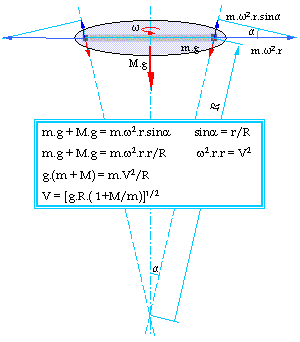
 Както се вижда от (рис.2) прибавянето на допълнителна маса може лесно да бъде компенсирано от известно увеличаване на скороста.

   В действителност, по вероятните конструкции за нашия летателен апарат биха изглеждали като дизайните на (рис.3 ляво), с два въртящи се в противоположни посоки пръстени, за да се компенсира помежду им реактивния момент, или като (рис.3 дясно) с двигатели директно задвижващи пръстена.

 

pic.2

  

pic3.

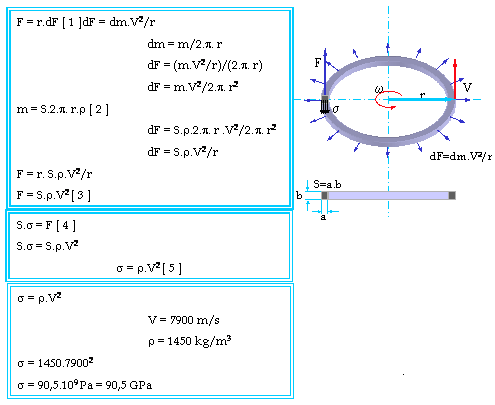
   Но нека продължим по-нататък, и да пресметнем на какви напрежения ще възникнат в един пръстен чиято периферна скорост е равна на орбиталната. Както вече знаем центробежната сила е равна на dF=dm.V2/r, и в нашия случай тя е разпределена равномерно по цялата обиколка, пораждайки вътрешни напрежения в тялото от които и се уравновесява.

   И тук е мястото където  трябва да ви обясня защо съм избрал точно тяло с форма  на пръстен.

   Едната от причините както може би вече се досещате е за опростяване  на пресмятанията, а другата е че, в радиалните сечения на тяло с такава форма под въздействие на центробежната сила възникват само нормални опънови напрежения s, които в същото време са винаги насочени в посока перпендикулярна на силата на тежестта и не влияят на равновесиeто на силите което разгледахме на (рис.1 ляво).

   Но да се върнем към пресмятанията.

pic.4
   След интегриране на dF по обиколката на пръстена, математически апарат с който не искам излишно да ви отeгчавам , получаваме силата F (рис.4 [ 1 ]), действаща във всяко едно от сеченията . Нека сега предположим че размерите a и b определящи площа на сечението S на пръстена са значително по-малки от радиса му r. Тогава ще е в сила израза (рис.4 [ 2 ]) за масата на пръстена, където S е площа на сечението а r обемната плътност на материала от който е изработен. Продължавайки по-нататък достигаме до равенството (рис.4 [ 3 ]). Както по-рано казахме силата F поражда и се уравновесява  в сеченията от силите на вътешните напрежения S.s , което ни довежда до равенство (рис.4 [ 4 ]), а след това и до (рис.4 [ 5 ]) s=r.V2.

  И отново размерите на пръстена нямат значение , единствено плътността на материала и периферната скорост са определящи за вътрешните напрежения!

  Въможно ли е всичко да се свежда  до това просто равенство? В действителност това беше началото, моментът след който се опитах да преосмисля всичко написано дотук и което ме наведе на ред итересни заключения. Но за тях ще е следващата страница.

   Сега да се върнем отново към формулите и заместим буквите с реални стойности. Орбиталната скорост за земята е V=7900 m/sec, и на пръстена да е изработен от материал с плътност  r=1450 kg/m3 (Kevlar). Тогава за вътрешните опънови напрежения се получава s=90,5 GPa! Гигантски, дори за (Kevlar) който издъжа 4 GPa, и е един от най-здравите материали които се произвеждат към настоящия момент. Ще са необходими материали 25 по-здрави от познатите ни днес преди да пристъпим към практическта реализация на подобни летателни апарати.

  Но да забравим за проблемите, бъдещето е близко и продължим към Nature of gravity.