On this, and on the next page I will try to explain to you my view about already mentioned articles
with the most common and simple mathematics possible.
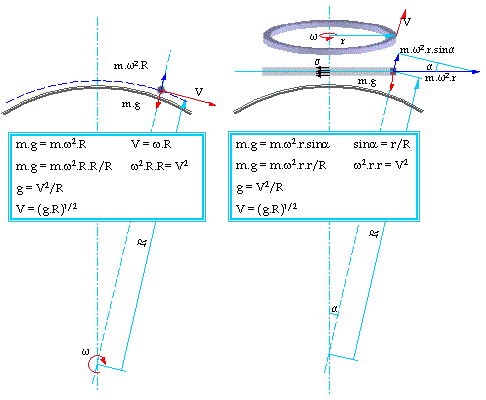
But first to make us clear with the general principle of orbital motion, let's start with classic case of object moving on an orbit around the world and forces acting upon it (pic.1 left).
These are, the force of gravity m.g and centrifugal force m.V2/R. The necessary condition to keep the object moving on the chosen orbit is these two forces to be equal. After some transformations (pic.1 left) we see, that the only condition necessary is, that the object moves with velocity V=(g.R)1/2(let call it orbital), with no sense of its mass.
Let's now take a look on forces acting upon a ring shaped body, with radius r and mass m which rotates with velocity V=w.r. Because the earth has spherical shape our ring is in the same time base of cone and each particle is on distance R from edge (center of earth), and upon each piece acts gravitational force m.g, and centrifugal force m.w2.r, and as we see from (pic.1 left) a small part of it m.w2.r.sina acts in direction opposite to gravitational force.
And at this point begins the interesting part. Let's see what is necessary to reach a balance between them? After short transformations (pic.1 left), again we find that the only condition necessary is, that the body moves with velocity V=(g.R)1/2. A familiar result that we have already achieved in the classic case of orbital motion.
Mass makes no sense, and also size of the ring , simply by reaching an orbital velocity our ring must start levitating!
pic.1
So far everything seems normal and we can tell that we have a propulsion for our flight system.
Further down we will take a look at some of the possible ways to create it, and difficulties that we may experience during realization of similar flight systems.
Actually, possible construction for our flight system would look more like designs on (pic.3 left), with two rotating in opposite directions rings, to compensate momentum, or like on (pic.3 right) with engines that turns the ring directly.
pic.2


pic.3
But let's go forward, and determine the stresses that appeared in ring rotating with orbital velocity. As we know centrifugal force is determined by dF=dm.V2/r, and acts on each piece generating internal stresses by which it is in fact compensated.
And here is the place where I must explain to you why I choose a body with exact ring shape.
One of the reasons is , as you may already guess is to make calculations as simple as possible , another is because, in radial sections of bodies with that shape, action of centrifugal force causes appearance of only normal tensile internal stresses s, which at the same time are always in direction normal to gravitational force and did not influence on the balance of forces on (pic.1 left).
But let's go back to calculations.
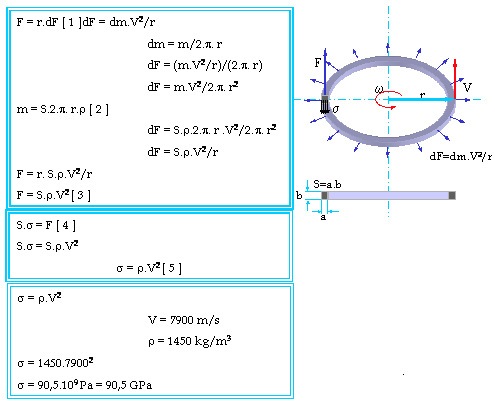
pic.4
And again sizes make no sense, only specific weight of material and velocity determine internal stresses!
Is it possible that everything reduces to this simple equation? In fact this was the beginning, the moment after which I have tried to rethink everything I have wrote so far, and which inspires some interesting conclusions. But about them will be next page.
Now let's go again back to formulas and replace letters with real values. Orbital velocity for earth is about V=7900 m/sec, and let the ring be made from material with specific weight r=1450 kg/m3 (Kevlar). Then for tensile internal stresses we have s=90,5 GPa! Gigantic, even for (Kevlar) witch is capable to sustain only 4 GPa and is one of the strongest materials produced at the moment. We will need materials 25 times stronger than these that we use today before we can take a step to real realization of similar flight systems.
But let's forget about problems, future is near and proceed to Nature of gravity.